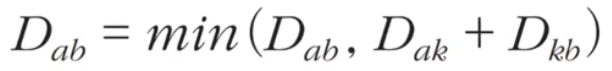플로이드 워셜 이란?

1. 플로이드 워셜 알고리즘의 개념

• 모든 노드에서 다른 노드 까지의 최단거리 경로를 모두 계산
• 다익스트라 알고리즘과 마찬가지로 단계별로 거쳐가는 노드를 기준으로 알고리즘을 수행
  • 하지만 매단계마다 방문하지 않은 노드중에 최단거리를 갖는 노드를 찾는 과정이 필요하지 않음
• 플로이드 워결은 2차원 테이블에 최단거리 정보를 저장
• 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속함

2. 알고리즘의 작동원리

• DP 기반의 알고리즘으로 점화식을 사용
• 각 단계마다 특정한 노들 k를 거쳐가는 경우를 확인
  • a 에서 b로 가는 최단거리보다 a 에서 k를 거쳐가는 b로 가는 거리가 더 짧은지 검사
  • 점화식
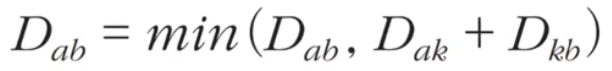
• 초기 상태에서는 그래프의 인접 행렬을 배열로 설정하며 자기 자신으로 가는 경로는 0으로 초기화 함

3. 플로이드 워셜 알고리즘의 단계

1. 초기화
   • 주어진 그래프의 가중치 행렬을 기반으로 배열을 초기화.
   • 자기자신으로 가는 경로는 0으로 연결되지 않는 경로는 무한대로 설정
2. 점화식 계산
   • 모든 정점 k에 대해 점화식을 반복
   • dist[i][j] = min(dist[][i]j, dist[i][k] + dist[k][j])
3. 음수 사이클 검사
   • 계산이 끝난후 배열의 대각선 원소 dist[i][i]를 확인
     • 만약 dist[i][i] < 0 인경우 정점 i 에서 시작하여 다시 정점 I로 돌아오는 경로에 음수 사이클이 존재한다는 것을 의미
     • 음수 사이클이 존재하면 최단 경로가 무의미 하므로 이에대한 예외처리가 필요

4. 구현 코드

import java.util.Arrays;
 
public class FloydWarshall {
 
    static final int INF = 1000000; // 무한대를 표현하기 위한 큰 값
 
    public static void floydWarshall(int[][] graph) {
        int n = graph.length;
        int[][] dist = new int[n][n];
 
        // 거리 배열 초기화
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dist[i][j] = graph[i][j];
            }
        }
 
        // 플로이드 워셜 점화식 적용
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (dist[i][k] != INF && dist[k][j] != INF) {
                        dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
                    }
                }
            }
        }
 
        // 결과 출력
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (dist[i][j] == INF) {
                    System.out.print("INF ");
                } else {
                    System.out.print(dist[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
 
    public static void main(String[] args) {
        int[][] graph = {
            {0, 3, INF, INF},
            {2, 0, INF, INF},
            {INF, 7, 0, 1},
            {6, INF, INF, 0}
        };
 
        floydWarshall(graph);
    }
}

5. 시간 복잡도

• 시간 복잡도는 N^3 임 따라서 노드의 수가 적을때 사용해야함
• 코딩테스트 문제에서는 보통 노드의 수를 500 이하로줌

6. 실제로 어쩔떄 쓰일까?

• 네트워크 라우팅 : 데이터 패킷 전송의 최적 경로를 계산
• 교통망 분석 : 도시간의 최단 이동 경로 계산
• 게임 계발 : 맵에서 NPC 간의 이동경로 계산